Floyd’s Cycle Detection

There is a famous algorithm called Floyd’s Cycle Detection Algorithm aka Tortoise and Hare Algorithm. It is used to detect a cycles in a list.

The tortoise is the slow pointer and the hare as fast pointer. The hare will travel in strides ot 2 while the tortoise will travel in stride of 1.

Image the following senario a linked list with a cycle.

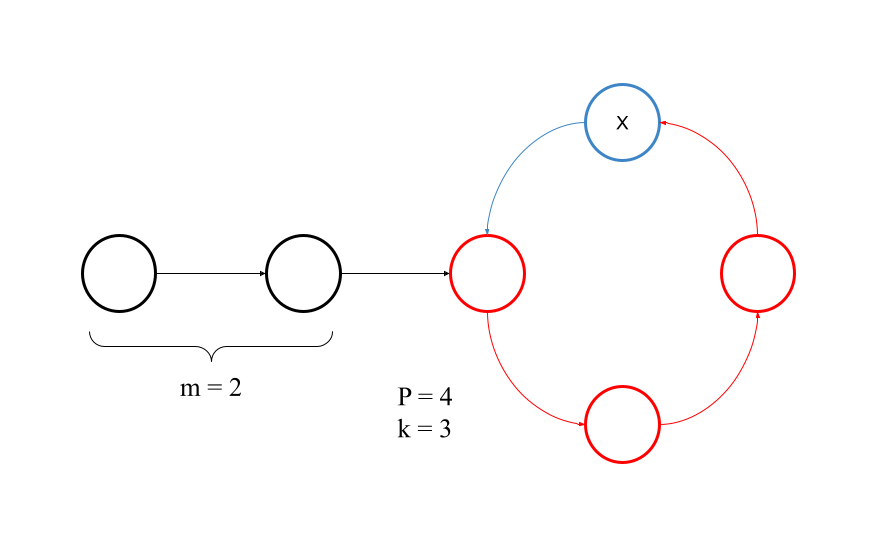
Some notation that we wiil use: $m$ is the distance from the start of the list to the start of the cycle, $P$ is the length of the cycle, and $k$ is the distance from the start of the cycle to the point where the hare and tortoise meet.

If one reached the end of the list, there is no cycles. If the two meet then there are 2 senarios that can happen:

$\Rightarrow \left\{ \begin{array}{ll} i=m+k+aP & \exist a \in \mathbb{Z} \\ j=m+k+bP & \exist b \in \mathbb{Z} \\ \end{array} \right.$

$\begin{aligned} a &:= \text{total loops the tortoise traveled} \\ b &:= \text{total loops the hare traveled} \\ i &:= \text{total distance tortoise traveled} \\ j &:= \text{total distance hare traveled} \end{aligned}$

Since the hare is traveling at twice the speed of the tortoise, if the two ever meet, the hare has traveled twice the distance. Therefore:

$j = 2i$

With some simple algebra

$\begin{aligned} m+k + bP &= 2((m+k) + aP) \\ m+k &= bP – 2aP \\ \Rightarrow i &= bP – 2aP + aP \\ &= bP – aP \end{aligned}$

The next step is to put the hare at the beginning of the cycles, but this time have both the tortoise and the hare take strides of 1. The point at which the 2 meet will be the start of the cycle.

Since the tortoise is currently at $(b-a)P$ when the hare travels $m$ steps:

1. The hare is at $m$
2. The tortoise is at $(b - a)P + m$

We can rearrange the tortoise to have traveled $m + (b - a)P$ or taking $m$ step then a integer multiple of $P$. Since there exits a cycles, traveling an integer multiple of $P$ around the cycles will land you at the beginning of the cycle.